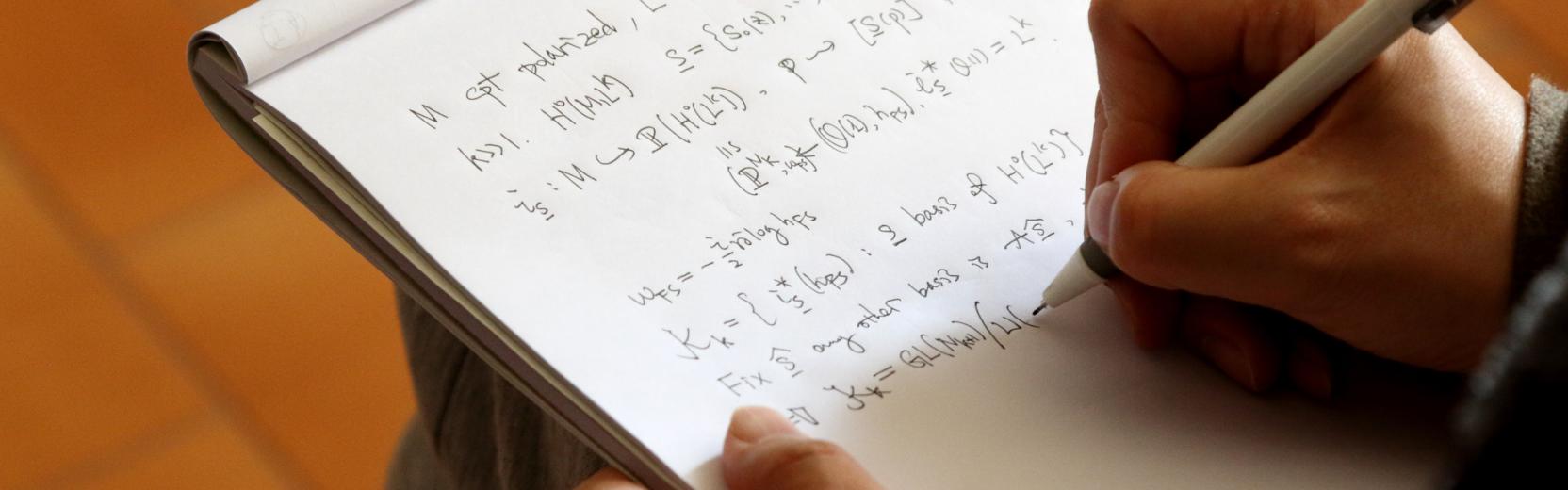Interview with 2024 Ramanujan Prize Winner

Ruochuan Liu of Peking University, China, was awarded the 2024 ICTP-IMU Ramanujan Prize “for his fundamental contributions to p-adic Hodge theory, especially his foundational study of relative p-adic Hodge theory and his remarkable work on rigidity and the Riemann-Hilbert correspondence for p-adic local systems”. He was presented with the award at a ceremony that took place on 9 December 2024 at ICTP, in the presence of Hélène Esnault of the Freie Universität Berlin, Germany, who introduced his work, and of Ulrike Tillmann, vice-president of the International Mathematical Union, which co-sponsors the award. At the ceremony, Liu gave a lecture entitled ‘Riemann-Hilbert for p-adic varieties’, and after the event he kindly agreed to answer a few questions about his life in mathematics.

What inspired you to study mathematics?

I have been good at math since I was a child and when I was about ten years old I was selected to attend some special classes used to offer to kids that were talented in mathematics. During class, which used to take place at the weekend, we were asked to solve problems similar to the ones that are given at the mathematical Olympiads, and soon I realised that I was good at that.

Books were also very important to me. I grew up in Shenyang, China, and my family used to live close to a library. I was interested in mathematics and I used to take advantage of my trips to the library to look for books about mathematics, which we did not have at home, since my parents were not particularly interested in the subject. A book that struck me is the Chinese translation of “Men of mathematics”, by Eric Temple Bell. The book recounts the lives and achievements of famous mathematicians such as Gauss, Euler, Riemann, Poincaré and Hilbert. I was very inspired by their biographies. Later on, I became particularly interested in elementary number theory and I would look for books on this specific topic. Thanks to those books I found out that I was good at solving problems in elementary number theory and I developed the confidence that I needed to keep doing it. I don’t think there was ever a specific moment when I decided to become a mathematician, I just naturally grew into one.

Something that was also very important for me is that my parents never forced me into a specific career direction. They just encouraged me to follow my heart and do the things I enjoyed. In China at that time, parents often make their own plans about the future of their children and they tend to impose their views on them. In this sense, my parents were different and I am very grateful for that. For sure, it helped that in our culture knowledge is respected and promoted and any career path that involves a lot of studying is regarded positively.

Scientists and mathematicians agree to say that the physical world is written in the mathematical language. However, it is often much more difficult to explain mathematical concepts in simple words than it is for other sciences, including theoretical physics. Why is that, in your opinion?

Math underlies every other science, and in that sense it is very special. However, differently from other sciences, mathematics does not deal with the real world, but it is about things that exists “in a world that lies behind the real world”. In some sense mathematics is deeper. Physics is also very deep and there are many aspects about physics that pertain to a world that is behind the real world, but in physics there is always a connection to the world we experience, which anyone can relate to.

Part of the difficulty in communicating mathematics is also due to the fact that mathematicians have a tendency to apply the same rigour they need in their daily job to the way they communicate, making it very difficult to convey mathematical ideas to the general audience. I think that by allowing ourselves to talk about mathematics in more approximate terms when we are not actually doing mathematics would help us convey the beauty of this discipline to other people.

Would you take up the challenge to explain what your research field is, in simple terms?

The most basic concept in my research is that of p-adic numbers, which are related to that of congruence. Two integers are congruent “modulo n” when their difference is exactly divisible by n. For example 8 is congruent to 3 modulo 5.

This is a very basic concept in number theory. Because of the structure of numbers, it is especially important to consider congruence modulo prime numbers. For example, modulo 3, modulo 5, modulo 7, et cetera. Of course things do not end there, one can also consider congruence modulo 3^2, modulo 3^3…

So if you fix a prime number, and call it p, you can look at all the numbers that are congruent modulo p, modulo p^2, modulo p^3, et cetera. In this way you can create a new system of numbers called p-adic numbers, inspired by considering congruence by the powers of primes. Once you create this new system of numbers, you can use your knowledge and intuition about real numbers in order to understand the characteristics of p-adic numbers.

What brought you to studying p-adic Hodge theory?

This was quite accidental. As a young Chinese mathematics undergraduate student 20 years ago, I was very delighted to be admitted to a university as prestigious as MIT. My main interest was in number theory and before getting there I did not have a clear idea of what professors at the MIT math department were doing there, but I quickly found out that there was no one working on algebraic number theory. However, I talked to Kiran Kedlaya, an arithmetic geometer who became my PhD advisor. I told him that I was very interested in the proof of Fermat’s last theorem, which had been a big inspiration for me to study number theory. He suggested me to read an introductory paper to  p-adic Hodge theory that was written by Laurent Berger. I found it very interesting and I just went on studying that more deeply.

Does that mean that you moved away from your original interest in number theory?

Yes and no. It is true that p-adic Hodge theory originated from arithmetic geometry, it has a geometrical origin but over the years it has developed into a broader subject with many applications to problems in number theory. The main line of my work is about developing tools that have their roots in the more geometric aspects of the theory in order to apply them to solve problems in number theory. In this sense, the work about Riemann-Hilbert for p-adic varieties that I presented during my lecture at the Ramanujan Prize Ceremony was a dream come true.

Have you already solved the problem you dreamt of solving or is there something left that you want to solve?

The p-adic Riemann-Hilbert correspondence was indeed the problem that I dreamt of solving, but there are some subsequent problems along the same lines that I am thinking of. I am also very interested in a new field that is developing fast at the moment, namely the interaction between p-adic geometry and algebraic topology. I have already done some work in this direction with my collaborators. I think it has connections with the Riemann-Hilbert problem, which I am willing to explore.

What is a math problem that you particularly struggled with and what made you choose to keep trying to solve it instead of moving on to something different?

When I was a PhD student at MIT I learnt about an interesting conjecture of Coleman about the eigencurve is proper. I thought that this was an interesting problem for me because it is about an object in number theory and I had a feeling that it could be solved by using p-adic Hodge theory. It seemed to be the perfect question for me. The strategy that I had in mind required me to generalise Harvard professor Mark Kisin’s famous work about the eigencurve, to begin with. I had the intuition that I shoud have the right background to generalize Kisin’s work. I kept working on this problem for years and when I was at the University of Michigan, already two years after my PhD, one night I suddenly realised that I knew how to generalise Kisin’s results by using techniques that I had learnt from my PhD advisor. That was a really exciting moment for me and I published the result soon. By using that result, together with my collaborators, I could prove that an eigencurve is proper. I think 4 or 5 years passed between the moment when I decided to start solving the problem and the moment when I actually solved it. During all this time I just kept believing that I could solve it.

How did you actually keep working on the problem for so long? Did you regularly set aside some time to go back to your desk and work on it?

For math problems like that, at the beginning you read as much literature as you can, in order to understand the problem. And at the very early stages, yes, you sit down at your desk and do calculations. But at some point, you become completely immersed in the question you are trying to solve and you can think about it anywhere at any time. For example, in this case, I found the answer late at night, while I was in bed, in that transitional state between sleep and wakefulness. The answer suddenly became clear in my mind. I did not even need to write it down immediately, I just knew it. This, however, doesn’t happen very often. Especially as you grow older it becomes more and more difficult to focus, because you have more and more to think about. 

What is the part of your life as a researcher that you enjoy the most?

The best part is of course that you can do what you want. This freedom is precious and unique to life in academia. At the beginning of one’s career as a researcher, that might not be completely true, but you still get a chance to work on problems that you find interesting. And the more established you become, the more freedom you develop to work even on crazy problems.

Did you ever doubt that you would become a mathematician?

I still doubt from time to time about what I will do. Math problems are very difficult and solving them implies a struggle. When you bump against your problem again and again, it is natural to start doubting of yourself. Doubt is a very common experience for mathematicians, even the most experienced ones.

What does the Ramanujan Prize mean to you?

This prize really came as a surprise. I knew about it, I just never thought that one day I would receive it. The day of the ceremony certainly was one of the most important in my life, I will not forget it. The prize recognizes my work at an international level, and I am proud of it. Taking part in the ceremony also gave me the opportunity to visit ICTP for the first time and it has been a very nice experience. ICTP is really a wonderful place and I hope to visit again in the future.

During the ceremony, Hélène Esnault shared a touching memory of meeting you as a student at Beijing University in 2003, when she was invited there to give a three-week lecture series. She recalled that you used to sit next to your fellow students in math, Chenyang Xu, who is now at Princeton University, and Zhiwei Yun, now at MIT, and that the three of you were enthusiastically asking questions from the very early morning. What do you remember of those days as a young student?

It was very touching for me to hear Prof. Esnault share those memories. This goes back to 20 years ago and reflecting on that time makes me think of how lucky I was. Back then China was not as rich, and its mathematical community not as thriving as it is today. So I realise now how fortunate I was to attend the lectures of a mathematician like Hélène Esnault when I was still an undergraduate. She was visiting with her husband, Eckart Viehweg, another great mathematician, and I feel very privileged to have met them at such a young age. The memory of me sitting beside Chenyang Xu and Zhiwei Yun also makes me feel very fortunate to have met two such good friends and great mathematicians. Having them by my side has helped me and has inspired me during my career.

At the ceremony, Ulrike Tillmann spoke of the foundational importance of basic science, and of mathematics in particular, for scientific, economical and societal development. She praised the investments in mathematics research made by China 20 years ago, which laid the seeds to the flourishing of a growing mathematical community. What ingredients does a country need to build a strong mathematical community?

Modern mathematics is becoming more and more technically complex and I think that in order to contribute successfully to research in the field, it is essential to rely on a large enough number of talented people, all working in the same place. A small number of leading top mathematicians are not enough. You may need a whole group of talented mathematicians instead.

I also think that mathematics should be promoted more and young people should be encouraged to take up this subject. The world is changing fast at the moment, young people have many options to choose from and it becomes more challenging to attract them to mathematics. I think that we should do more to convey the beauty of mathematics to the general audience. Mathematicians tend to stay in their comfort zone and, as a community, we should do more to communicate with the rest of the world. This has two benefits: it would allow to attract young talents and it would also help to convince funders to support mathematics research. It is true that mathematicians do not need much money to do their work, but we still need some.

Pictures of the 2024 Ramanujan Prize Ceremony can be found on ICTP's Flickr page.